Jump to content

Portal:Mathematics

Page semi-protected
From Wikipedia, the free encyclopedia

Portal topics
Activities
Culture
Geography
Health
History
Mathematics
Nature
People
Philosophy
Religion
Society
Technology
Random portal
edit 

The Mathematics Portal

Shortcuts

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

  Featured articles are displayed here, which represent some of the best content on English Wikipedia.
More featured articles
edit 

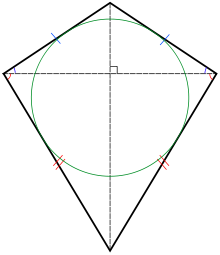
Selected image – show another

a smooth surface, vaguely conical in shape and embedded in a basket-like mesh of points, rotates in empty space
a smooth surface, vaguely conical in shape and embedded in a basket-like mesh of points, rotates in empty space
Non-uniform rational B-splines (NURBS) are commonly used in computer graphics for generating and representing curves and surfaces for both analytic shapes (described by mathematical formulas) and modeled shapes. Here the shape of the surface is determined by control points, shown as small spheres surrounding the surface itself. The square at the bottom sets the maximum width and length of the surface. Based on early work by Pierre Bézier and Paul de Casteljau, NURBS are generalizations of both B-splines (basis splines) and Bézier curves and surfaces. Unlike simple Bézier curves and surfaces, which are non-rational, NURBS can represent exactly certain analytic shapes such as conic sections and spherical sections. They are widely used in computer-aided design (CAD), manufacturing (CAM), and engineering (CAE), although T-splines and subdivision surfaces may be more suitable for more complex organic shapes.

Good articles – load new batch

  These are Good articles, which meet a core set of high editorial standards.
  • Image 1 In control system theory, and various branches of engineering, a transfer function matrix, or just transfer matrix is a generalisation of the transfer functions of single-input single-output (SISO) systems to multiple-input and multiple-output (MIMO) systems. The matrix relates the outputs of the system to its inputs. It is a particularly useful construction for linear time-invariant (LTI) systems because it can be expressed in terms of the s-plane. In some systems, especially ones consisting entirely of passive components, it can be ambiguous which variables are inputs and which are outputs. In electrical engineering, a common scheme is to gather all the voltage variables on one side and all the current variables on the other regardless of which are inputs or outputs. This results in all the elements of the transfer matrix being in units of impedance. The concept of impedance (and hence impedance matrices) has been borrowed into other energy domains by analogy, especially mechanics and acoustics. (Full article...)
    In control system theory, and various branches of engineering, a transfer function matrix, or just transfer matrix is a generalisation of the transfer functions of single-input single-output (SISO) systems to multiple-input and multiple-output (MIMO) systems. The matrix relates the outputs of the system to its inputs. It is a particularly useful construction for linear time-invariant (LTI) systems because it can be expressed in terms of the s-plane.

    In some systems, especially ones consisting entirely of passive components, it can be ambiguous which variables are inputs and which are outputs. In electrical engineering, a common scheme is to gather all the voltage variables on one side and all the current variables on the other regardless of which are inputs or outputs. This results in all the elements of the transfer matrix being in units of impedance. The concept of impedance (and hence impedance matrices) has been borrowed into other energy domains by analogy, especially mechanics and acoustics. (Full article...)
  • Image 2 A kite, showing its pairs of equal-length sides and its inscribed circle. In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, with two diagonal axes of symmetry; and the squares, which are also special cases of both right kites and rhombi. (Full article...)

    A kite, showing its pairs of equal-length sides and its inscribed circle.

    In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

    Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, with two diagonal axes of symmetry; and the squares, which are also special cases of both right kites and rhombi. (Full article...)
  • Image 3 A Pythagorean tiling A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern, but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern. This tiling has four-way rotational symmetry around each of its squares. When the ratio of the side lengths of the two squares is an irrational number such as the golden ratio, its cross-sections form aperiodic sequences with a similar recursive structure to the Fibonacci word. Generalizations of this tiling to three dimensions have also been studied. (Full article...)
    A Pythagorean tiling

    A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern,
    but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.

    This tiling has four-way rotational symmetry around each of its squares. When the ratio of the side lengths of the two squares is an irrational number such as the golden ratio, its cross-sections form aperiodic sequences with a similar recursive structure to the Fibonacci word. Generalizations of this tiling to three dimensions have also been studied. (Full article...)
  • Image 4 The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle. All points on a side are equidistant from the opposite vertex. A Reuleaux triangle [ʁœlo] is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?" They are named after Franz Reuleaux, a 19th-century German engineer who pioneered the study of machines for translating one type of motion into another, and who used Reuleaux triangles in his designs. However, these shapes were known before his time, for instance by the designers of Gothic church windows, by Leonardo da Vinci, who used it for a map projection, and by Leonhard Euler in his study of constant-width shapes. Other applications of the Reuleaux triangle include giving the shape to guitar picks, fire hydrant nuts, pencils, and drill bits for drilling filleted square holes, as well as in graphic design in the shapes of some signs and corporate logos. (Full article...)
    The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle. All points on a side are equidistant from the opposite vertex.

    A Reuleaux triangle [ʁœlo] is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

    They are named after Franz Reuleaux, a 19th-century German engineer who pioneered the study of machines for translating one type of motion into another, and who used Reuleaux triangles in his designs. However, these shapes were known before his time, for instance by the designers of Gothic church windows, by Leonardo da Vinci, who used it for a map projection, and by Leonhard Euler in his study of constant-width shapes. Other applications of the Reuleaux triangle include giving the shape to guitar picks, fire hydrant nuts, pencils, and drill bits for drilling filleted square holes, as well as in graphic design in the shapes of some signs and corporate logos. (Full article...)
  • Image 5 Natural patterns form as wind blows sand in the dunes of the Namib Desert. The crescent shaped dunes and the ripples on their surfaces repeat wherever there are suitable conditions. Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time. In the 19th century, the Belgian physicist Joseph Plateau examined soap films, leading him to formulate the concept of a minimal surface. The German biologist and artist Ernst Haeckel painted hundreds of marine organisms to emphasise their symmetry. Scottish biologist D'Arcy Thompson pioneered the study of growth patterns in both plants and animals, showing that simple equations could explain spiral growth. In the 20th century, the British mathematician Alan Turing predicted mechanisms of morphogenesis which give rise to patterns of spots and stripes. The Hungarian biologist Aristid Lindenmayer and the French American mathematician Benoît Mandelbrot showed how the mathematics of fractals could create plant growth patterns. (Full article...)
    Natural patterns form as wind blows sand in the dunes of the Namib Desert. The crescent shaped dunes and the ripples on their surfaces repeat wherever there are suitable conditions.

    Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.

    In the 19th century, the Belgian physicist Joseph Plateau examined soap films, leading him to formulate the concept of a minimal surface. The German biologist and artist Ernst Haeckel painted hundreds of marine organisms to emphasise their symmetry. Scottish biologist D'Arcy Thompson pioneered the study of growth patterns in both plants and animals, showing that simple equations could explain spiral growth. In the 20th century, the British mathematician Alan Turing predicted mechanisms of morphogenesis which give rise to patterns of spots and stripes. The Hungarian biologist Aristid Lindenmayer and the French American mathematician Benoît Mandelbrot showed how the mathematics of fractals could create plant growth patterns. (Full article...)
  • Image 6 The Euclid–Euler theorem is a theorem in number theory that relates perfect numbers to Mersenne primes. It states that an even number is perfect if and only if it has the form 2p−1(2p − 1), where 2p − 1 is a prime number. The theorem is named after mathematicians Euclid and Leonhard Euler, who respectively proved the "if" and "only if" aspects of the theorem. It has been conjectured that there are infinitely many Mersenne primes. Although the truth of this conjecture remains unknown, it is equivalent, by the Euclid–Euler theorem, to the conjecture that there are infinitely many even perfect numbers. However, it is also unknown whether there exists even a single odd perfect number. (Full article...)
    The Euclid–Euler theorem is a theorem in number theory that relates perfect numbers to Mersenne primes. It states that an even number is perfect if and only if it has the form 2p−1(2p − 1), where 2p − 1 is a prime number. The theorem is named after mathematicians Euclid and Leonhard Euler, who respectively proved the "if" and "only if" aspects of the theorem.

    It has been conjectured that there are infinitely many Mersenne primes. Although the truth of this conjecture remains unknown, it is equivalent, by the Euclid–Euler theorem, to the conjecture that there are infinitely many even perfect numbers. However, it is also unknown whether there exists even a single odd perfect number. (Full article...)
  • Image 7 Selected witch of Agnesi curves (green), and the circles they are constructed from (blue), with radius parameters '"`UNIQ--postMath-00000005-QINU`"', '"`UNIQ--postMath-00000006-QINU`"', '"`UNIQ--postMath-00000007-QINU`"', and '"`UNIQ--postMath-00000008-QINU`"'. In mathematics, the witch of Agnesi (Italian pronunciation: [aɲˈɲeːzi, -eːsi; -ɛːzi]) is a cubic plane curve defined from two diametrically opposite points of a circle. The curve was studied as early as 1653 by Pierre de Fermat, in 1703 by Guido Grandi, and by Isaac Newton. It gets its name from Italian mathematician Maria Gaetana Agnesi who published it in 1748. The Italian name la versiera di Agnesi is based on Latin versoria (sheet of sailing ships) and the sinus versus. This was read by John Colson as l’avversiera di Agnesi, where avversiera is translated as "woman who is against God" and interpreted as "witch". (Full article...)
    Selected witch of Agnesi curves (green), and the circles they are constructed from (blue), with radius parameters , , , and .


    In mathematics, the witch of Agnesi (Italian pronunciation: [aɲˈɲeːzi, -eːsi; -ɛːzi]) is a cubic plane curve defined from two diametrically opposite points of a circle.

    The curve was studied as early as 1653 by Pierre de Fermat, in 1703 by Guido Grandi, and by Isaac Newton. It gets its name from Italian mathematician Maria Gaetana Agnesi who published it in 1748. The Italian name la versiera di Agnesi is based on Latin versoria (sheet of sailing ships) and the sinus versus.
    This was read by John Colson as l’avversiera di Agnesi, where avversiera is translated as "woman who is against God" and interpreted as "witch". (Full article...)
  • Image 8 In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. This result provides a classification theorem for the three-dimensional convex polyhedra, something that is not known in higher dimensions. It provides a complete and purely combinatorial description of the graphs of these polyhedra, allowing other results on them, such as Eberhard's theorem on the realization of polyhedra with given types of faces, to be proven more easily, without reference to the geometry of these shapes. Additionally, it has been applied in graph drawing, as a way to construct three-dimensional visualizations of abstract graphs. Branko Grünbaum has called this theorem "the most important and deepest known result on 3-polytopes." (Full article...)
    In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

    This result provides a classification theorem for the three-dimensional convex polyhedra, something that is not known in higher dimensions. It provides a complete and purely combinatorial description of the graphs of these polyhedra, allowing other results on them, such as Eberhard's theorem on the realization of polyhedra with given types of faces, to be proven more easily, without reference to the geometry of these shapes. Additionally, it has been applied in graph drawing, as a way to construct three-dimensional visualizations of abstract graphs. Branko Grünbaum has called this theorem "the most important and deepest known result on 3-polytopes." (Full article...)
  • Image 9 Richard Wesley Hamming (February 11, 1915 – January 7, 1998) was an American mathematician whose work had many implications for computer engineering and telecommunications. His contributions include the Hamming code (which makes use of a Hamming matrix), the Hamming window, Hamming numbers, sphere-packing (or Hamming bound), Hamming graph concepts, and the Hamming distance. Born in Chicago, Hamming attended University of Chicago, University of Nebraska and the University of Illinois at Urbana–Champaign, where he wrote his doctoral thesis in mathematics under the supervision of Waldemar Trjitzinsky (1901–1973). In April 1945, he joined the Manhattan Project at the Los Alamos Laboratory, where he programmed the IBM calculating machines that computed the solution to equations provided by the project's physicists. He left to join the Bell Telephone Laboratories in 1946. Over the next fifteen years, he was involved in nearly all of the laboratories' most prominent achievements. For his work, he received the Turing Award in 1968, being its third recipient. (Full article...)
    Richard Wesley Hamming (February 11, 1915 – January 7, 1998) was an American mathematician whose work had many implications for computer engineering and telecommunications. His contributions include the Hamming code (which makes use of a Hamming matrix), the Hamming window, Hamming numbers, sphere-packing (or Hamming bound), Hamming graph concepts, and the Hamming distance.

    Born in Chicago, Hamming attended University of Chicago, University of Nebraska and the University of Illinois at Urbana–Champaign, where he wrote his doctoral thesis in mathematics under the supervision of Waldemar Trjitzinsky (1901–1973). In April 1945, he joined the Manhattan Project at the Los Alamos Laboratory, where he programmed the IBM calculating machines that computed the solution to equations provided by the project's physicists. He left to join the Bell Telephone Laboratories in 1946. Over the next fifteen years, he was involved in nearly all of the laboratories' most prominent achievements. For his work, he received the Turing Award in 1968, being its third recipient. (Full article...)
  • Image 10 The mutilated chessboard The mutilated chessboard problem is a tiling puzzle posed by Max Black in 1946 that asks: Suppose a standard 8×8 chessboard (or checkerboard) has two diagonally opposite corners removed, leaving 62 squares. Is it possible to place 31 dominoes of size 2×1 so as to cover all of these squares? (Full article...)
    The mutilated chessboard

    The mutilated chessboard problem is a tiling puzzle posed by Max Black in 1946 that asks:

    Suppose a standard 8×8 chessboard (or checkerboard) has two diagonally opposite corners removed, leaving 62 squares. Is it possible to place 31 dominoes of size 2×1 so as to cover all of these squares?

    (Full article...)
  • Image 11 The square root of 2 is equal to the length of the hypotenuse of a right triangle with legs of length 1 and is therefore a constructible number In geometry and algebra, a real number '"`UNIQ--postMath-00000009-QINU`"' is constructible if and only if, given a line segment of unit length, a line segment of length '"`UNIQ--postMath-0000000A-QINU`"' can be constructed with compass and straightedge in a finite number of steps. Equivalently, '"`UNIQ--postMath-0000000B-QINU`"' is constructible if and only if there is a closed-form expression for '"`UNIQ--postMath-0000000C-QINU`"' using only integers and the operations for addition, subtraction, multiplication, division, and square roots. The geometric definition of constructible numbers motivates a corresponding definition of constructible points, which can again be described either geometrically or algebraically. A point is constructible if it can be produced as one of the points of a compass and straightedge construction (an endpoint of a line segment or crossing point of two lines or circles), starting from a given unit length segment. Alternatively and equivalently, taking the two endpoints of the given segment to be the points (0, 0) and (1, 0) of a Cartesian coordinate system, a point is constructible if and only if its Cartesian coordinates are both constructible numbers.[1] Constructible numbers and points have also been called ruler and compass numbers and ruler and compass points, to distinguish them from numbers and points that may be constructed using other processes. (Full article...)
    The square root of 2 is equal to the length of the hypotenuse of a right triangle with legs of length 1 and is therefore a constructible number


    In geometry and algebra, a real number is constructible if and only if, given a line segment of unit length, a line segment of length can be constructed with compass and straightedge in a finite number of steps. Equivalently, is constructible if and only if there is a closed-form expression for using only integers and the operations for addition, subtraction, multiplication, division, and square roots.

    The geometric definition of constructible numbers motivates a corresponding definition of constructible points, which can again be described either geometrically or algebraically. A point is constructible if it can be produced as one of the points of a compass and straightedge construction (an endpoint of a line segment or crossing point of two lines or circles), starting from a given unit length segment. Alternatively and equivalently, taking the two endpoints of the given segment to be the points (0, 0) and (1, 0) of a Cartesian coordinate system, a point is constructible if and only if its Cartesian coordinates are both constructible numbers.[1] Constructible numbers and points have also been called ruler and compass numbers and ruler and compass points, to distinguish them from numbers and points that may be constructed using other processes. (Full article...)
  • Image 12 A three-page book embedding of the complete graph K5. Because it is not a planar graph, it is not possible to embed this graph without crossings on fewer pages, so its book thickness is three. In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number. Every graph with n vertices has book thickness at most '"`UNIQ--postMath-0000000D-QINU`"', and this formula gives the exact book thickness for complete graphs. The graphs with book thickness one are the outerplanar graphs. The graphs with book thickness at most two are the subhamiltonian graphs, which are always planar; more generally, every planar graph has book thickness at most four. It is NP-hard to determine the exact book thickness of a given graph, with or without knowing a fixed vertex ordering along the spine of the book. Testing the existence of a three-page book embedding of a graph, given a fixed ordering of the vertices along the spine of the embedding, has unknown computational complexity: it is neither known to be solvable in polynomial time nor known to be NP-hard. (Full article...)
    A three-page book embedding of the complete graph K5. Because it is not a planar graph, it is not possible to embed this graph without crossings on fewer pages, so its book thickness is three.

    In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.

    Every graph with n vertices has book thickness at most , and this formula gives the exact book thickness for complete graphs. The graphs with book thickness one are the outerplanar graphs. The graphs with book thickness at most two are the subhamiltonian graphs, which are always planar; more generally, every planar graph has book thickness at most four. It is NP-hard to determine the exact book thickness of a given graph, with or without knowing a fixed vertex ordering along the spine of the book. Testing the existence of a three-page book embedding of a graph, given a fixed ordering of the vertices along the spine of the embedding, has unknown computational complexity: it is neither known to be solvable in polynomial time nor known to be NP-hard. (Full article...)
More good articles

Did you know (auto-generated) – load new batch

edit 

More did you know – view different entries

Did you know...
Did you know...
More did you know facts
Showing 7 items out of 75
edit 

Selected article – show another

A Hilbert space is a real or complex vector space with a positive-definite Hermitian form, that is complete under its norm. Thus it is an inner product space, which means that it has notions of distance and of angle (especially the notion of orthogonality or perpendicularity). The completeness requirement ensures that for infinite dimensional Hilbert spaces the limits exist when expected, which facilitates various definitions from calculus. A typical example of a Hilbert space is the space of square summable sequences.

Hilbert spaces allow simple geometric concepts, like projection and change of basis to be applied to infinite dimensional spaces, such as function spaces. They provide a context with which to formalize and generalize the concepts of the Fourier series in terms of arbitrary orthogonal polynomials and of the Fourier transform, which are central concepts from functional analysis. Hilbert spaces are of crucial importance in the mathematical formulation of quantum mechanics. (Full article...)

View all selected articles
edit 

Subcategories

Full category tree. Select [►] to view subcategories.
Mathematics
Mathematics by country
Fields of mathematics
Mathematics-related lists
Mathematicians
Women in mathematics
Works about mathematics
Mathematics and art
Mathematical classification systems
Mathematical concepts
Mathematical constants
Mathematics and culture
Eponyms in mathematics
Mathematical examples
FL-Class Polyhedra articles
History of mathematics
Mathematical notation
Mathematical science occupations
Outlines of mathematics and logic
Philosophy of mathematics
Mathematical projects
Mathematical proofs
Pseudomathematics
Set index articles on mathematics
Mathematical terminology
Mathematical theorems
Mathematical tools
Mathematics stubs
More mathematics categories
edit 

Topics in mathematics

General Foundations Number theory Discrete mathematics


Algebra Analysis Geometry and topology Applied mathematics
Source
edit 

Index of mathematics articles

ARTICLE INDEX:
MATHEMATICIANS:
edit 
edit 

WikiProjects

WikiProjects The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.

In other Wikimedia projects

The following Wikimedia Foundation sister projects provide more on this subject:

More portals

  1. ^ Kazarinoff (2003), pp. 10, 15; Martin (1998), p. 41, Corollary 2.16.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Portal:Mathematics&oldid=1246080347"